一个地方的气压值经常有变化，变化的根本原因是其上空大气柱中空气质量的增多或减少。大气柱质量的增减又往往是大气柱厚度和密度改变的反映。当气柱增厚、密度增大时，则空气质量增多，气压就升高。反之，气压则减小。因而，任何地方的气压值总是随着海拔高度的增高而递减。如图4•1所示，甲气柱从地面到1000m和从1000m到

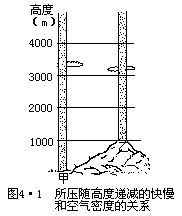
2000m，虽然都是减少同样高度的气柱，但是低层空气密度大于高层，因而低层气压降低的数值大于高层。据实测，在地面层中，高度每升100m，气压平均降低12.7hPa，在高层则小于此数值。确定空气密度大小与气压随高度变化的定量关系，一般是应用静力学方程和压高方程。
（一）静力学方程
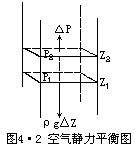
假设大气相对于地面处于静止状态，则某一点的气压值等于该点单位面积上所承受铅直气柱的重量。见图4•2，在大气柱中截取面积为1cm2，厚度为△Z的薄气柱。设高度Z1处的气压为P1，高度Z2处的气压为P2，空气密度为ρ，重力加速度为g。在静力平衡条件下，Z1面上的气压P1和Z2面上的气压P2间的气压差应等于这两个高度面间的薄气柱重量，即
P2-P1=-△P=-ρg（Z2-Z1）=-ρg△Z
式中负号表示随高度增高，气压降低。若△Z趋于无限小，则上式可写成
-dP=ρgdZ （4.1）
上式是气象上应用的大气静力学方程。方程说明，气压随高度递减的快慢取决于空气密度（ρ）和重力加速度（g）的变化。重力加速度（g）随高度的变化量一般很小，因而气压随高度递减的快慢主要决定于空气的密度。在密度大的气层里，气压随高递减得快，反之则递减得慢。实践证明，静力学方程虽是静止大气的理论方程，但除在有强烈对流运动的局部地区外，其误差仅有1％，因而得到广泛应用。将（4•1）式变换




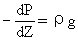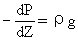
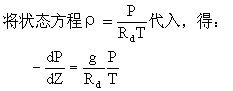
高度所降低的气压值。
实际工作中还经常引用气压高度差（h），它表示在铅直气柱中气压每改变一个单位所对应的高度变化值。显然它是铅直气压梯度的倒数，即

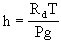
式中Rd=287J/kgK为干空气的气体常数。将Rd、g值代入，并将T换成摄氏温标t，则得

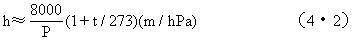
表4•l是根据（4•2）式计算出的不同气温和气压下的h值。

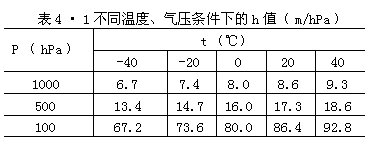
从表4•l中可以看出：①在同一气压下，气柱的温度愈高，密度愈小，气压随高度递减得愈缓慢，单位气压高度差愈大。反之，气柱温度愈低，单位气压高度差愈小。②在同一气温下，气压值愈大的地方，空气密度愈大，气压随高度递减得愈快，单位高度差愈小。反之，气压愈低的地方单位气压高度差愈大。比如愈到高空，空气愈稀薄，虽然同样取上下气压差一个百帕，而气柱厚度却随高度而迅速增大。
通常，大气总处于静力平衡状态，当气层不太厚和要求精度不太高时，（4•2）式可以用来粗略地估算气压与高度间的定量关系，或者用于将地面气压订正为海平面气压。如果研究的气层高度变化范围很大，气柱中上下层温度、密度变化显著时，该式就难以直接运用，就需采用适合于较大范围气压随高度变化的关系式，即压高方程。
（二）压高方程
为了精确地获得气压与高度的对应关系，通常将静力学方程从气层底部到顶部进行积分，即得出压高方程

式中，P1、P2分别是高度Z1和Z2的气压值。该式表示任意两个高度上的气压差等于这两个高度间单位截面积空气柱的重量。用状态方程替换式中的ρ，得
（4•4）式是通用的压高方程。它表示气压是随高度的增加而按指数递减的规律。而且在大气低层，气压递减得快，在高层递减得慢。在温度低时，气压递减得快，在温度高时，递减得慢。利用（4•4）式原则上可以进行气压和高度间的换算，但直接计算还比较困难。因为在公式中指数上的子式中，g和T都随高度而有变化，而且R因不同高度上空气组成的差异也会随高度而变化，因而进行积分是困难的。为了方便实际应用，需要对方程作某些特定假设。比如忽略重力加速度的变化和水汽影响，并假定气温不随高度发生变化，此条件下的压高方程，称为等温大气压高方程。在等温大气中，（4•4）式中的T可视为常数，于是得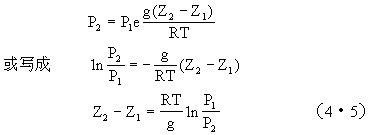
式中负号取消是因为将P1和P2的位置上下调换。从（4•5）式中可以看出，等温大气中，气压随高度仍是按指数规律递减的，其变化曲线见图4•3中实线。将T换成t，自然对数换成常用对数，并将g、R代入，则（4•5）式变成气象上常用的等温大气压高方程：
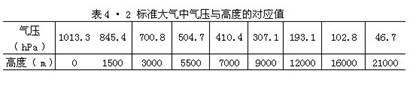
实际大气并非等温大气，所以应用（4•6）式计算实际大气的厚度和高度时，必须将大气划分为许多薄层，求出每个薄层的tm，然后分别计算各薄层的厚度，最后把各薄层的厚度求和便是实际大气的厚度。表4•2是利用（4•6）式计算的标准大气中气压与高度的对应值。

（4.6）式中把重力加速度g当成常数，实际上g随纬度和高度而有变化，要求得精确的Z值，还必须对g作纬度和高度的订正。一般说，在大气低层g随高度的变化不大，但将此式应用到100km以上的高层大气时，就必须考虑g的变化。此外，（4•6）式是把大气当成干空气处理的，但当空气中水汽含量较多时，就必须用虚温代替式中的气温。
假设温度直减率（γ）不随高度变化的大气称多元大气。若取海平面的气温为T0，于是任意高度Z处的气温T=T0-γZ。令Z0=0，海平面气压为P0，任意高度Z上的气压为Pz，应用（4•4）式有

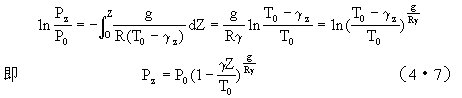
（4•7）式表示在多元大气中，气压随高度也是按指数规律递减的。当γ=0.6℃/100m，T0=273K，P0=1000hPa时，气压随高度降低的情况如图4•3中的虚线所示。图中实线是等温大气的情况，其气压随高度的递减比多元大气慢一些。实际大气与多元大气更为接近。

　

[设本页为书签]